How to use Regency's lighting calculator: Calculating energy savings from a lighting retrofit

Lighting conversion math isn't simple. There are a lot of variables to consider. And if you're working toward getting money allocated in the budget for a retrofit project, your boss will likely be looking for several different numbers, from payback period to estimated monthly savings and more.

Where do you begin?

We built a lighting retrofit calculator that should help you to get your head around the basics.

Here's what you'll need to have handy to use it:

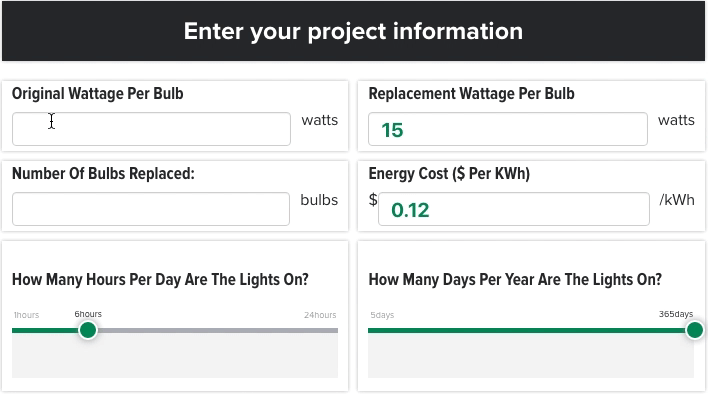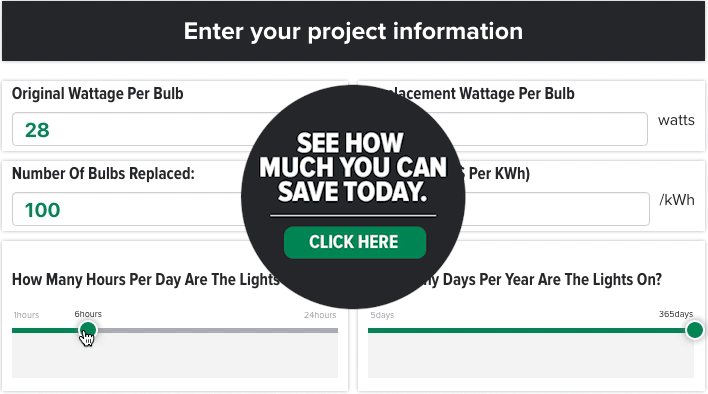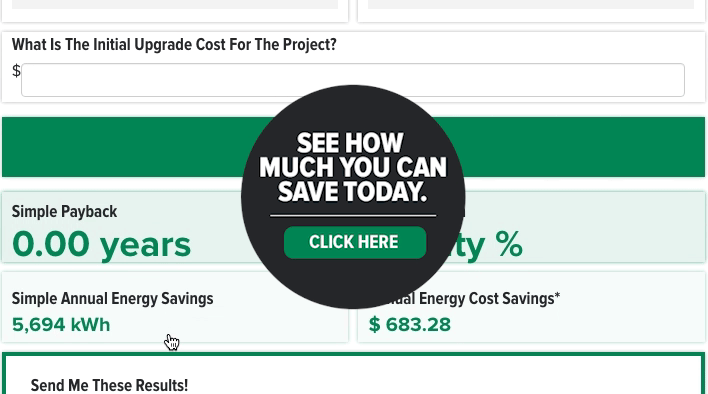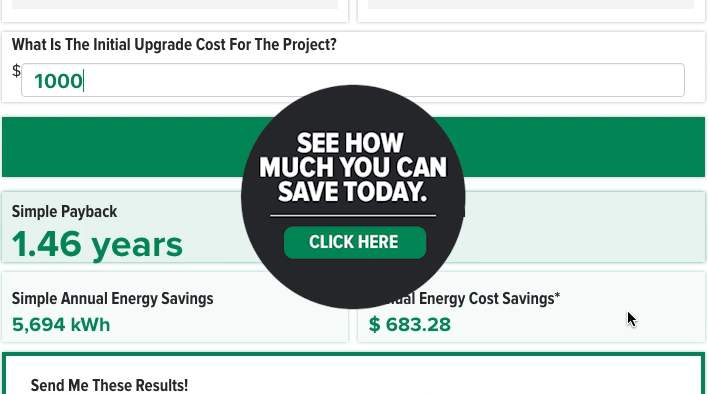
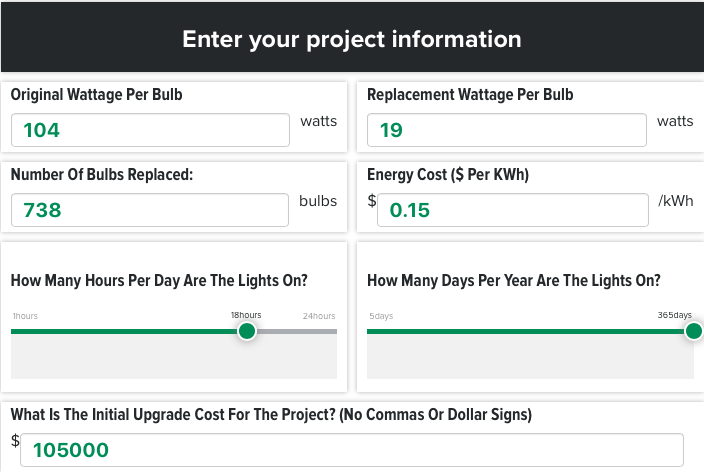
Original wattage per bulb: Which lamps are being replaced? How much wattage do they consume?

Note: if you're doing a complete retrofit involving multiple lamp types, plug them into the calculator individually. You may also find our post about lighting audits handy, which you can find here.

Replacement wattage per bulb: What is the wattage of the replacement bulbs?

If you have ballast-dependent fixtures with multiple lamps to retrofit, you should use total fixture wattage in the original wattage and replacement wattage fields and include ballast factor and all lamp wattage in your figures.

If you need a guide when it comes to calculating ballast factor, click here.

As an example, if you have three-lamp fluorescent troffers, and each lamp consumes 28 W, total fixture wattage would come out to 73.92 W, assuming a normal ballast factor.

The math breaks down like this:

28 W x 3 lamps x 0.88 (normal ballast factor/ draw) = 73.92 W

Check out our post, "What is a ballast factor and how does it affect my fluorescent tubes?" for more.

Number of bulbs replaced: Have you audited your space to determine how many lamps will be replaced? Count them up, and make sure they're all the same type to get the most accurate savings estimate.

Cost of energy: Reference your electric bill to determine how much your energy is costing you. In general, rates fall between $0.06/ kWh to $0.24/ kWh, depending on the demand in the area you live, though there are certainly outliers on both ends of the spectrum.

Learn more: kW vs. kWh: How much energy is my lighting using?

Need help converting watts to kWh? We built a calculator for that, too.

Daily "on" hours: How many hours are the lights burning per day, on average?

Annual "on" days: How many days per year are the lights burning?

Initial cost of upgrade: Include material costs and, as an option, the cost of labor, if you're hiring outside labor to complete the project.

Okay, do you have all of that information gathered?

See the screenshot below for reference.

Screen Shot 2017-01-13 at 2.48.12 PM.png

Looking to get more detailed calculations? Download our Ultimate Guide to Energy Savings Calculations and Payback to understand how a lighting retrofit could save you on the cost of HVAC, labor, and material costs, in addition to the cost of energy.

Once you have entered your project information, it's time to calculate ROI for your lighting project.

Here's what our calculator will produce, in terms of ROI calculations, and how you should understand them:

Simple payback: This is a very high-level look at the outcome of your project. Simple payback is how long it will take you to earn back the cost of upfront investment through savings.

Simple annual energy savings: Expressed in kWh, this is how much energy a lighting retrofit would save in energy over the course of a year.

Annual energy cost savings: The calculator will take the figure above (annual energy savings) and multiply it by your cost of energy to calculate just how much you could save monthly after completing the project. This number does not take into account the upfront cost of your project.

Rate of return: Our calculator is built to give you a first-year rate of return on your project, expressed as a percentage. So, if your retrofit project costs $20,000 up-front and you save $1,000 on energy every month after its completion, your rate of return would be 60 percent, as you would have made back $12,000 in savings, which is 60 percent of the upfront cost of the project.

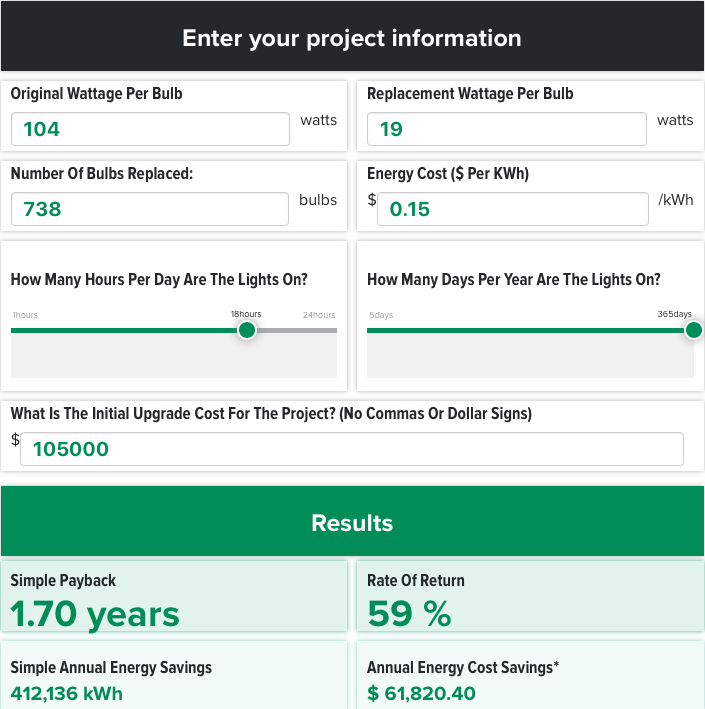
Screen Shot 2017-01-13 at 2.08.33 PM.png

If this kind of return seems impossible, it's not. Check out how one hotel we worked with saw the return above when they retrofitted to LED.

Our lighting calculator is designed to be a gut check on whether or not a retrofit makes sense for you. But a complete lighting conversion analysis would show that there are more savings to be had, in the form of savings.

We put together a resource to help you perform more detailed calculations, called The Ultimate Guide to Energy Savings Calculations, Payback and ROI.

Download it below: